
In this two-part series, I want to take a functional approach to building React applications.
There will be mathematical theory sprinkled throughout the series, and hopefully by the end of it you will pick up some useful techniques!
Series contents:
- Part 1 - Deconstructing the React Component
- Part 2 - The Reader monad and read-only context
Functional programming – category theory in particular – teaches us a lot about program construction. Much of the tools that functional programmers reach for are very generalized, and widely applicable to various domains. It is this learn once, appy everywhere idea that I think would appeal to many folks in the business of making software. (Not to mention that functional programming is fun!)
React has many patterns that grew out of the community. I want to take a step back and view these patterns from a new angle, and see if we can formalize them with mathematical theory.
You will need basic React knowledge in order to understand this series. I will discuss concepts such as components, elements, and higher-order components (HOC).
If you want to jump ahead a bit, the repository with the final, full examples are on GitHub. Word of warning though, there isn’t much documentation, so it’s probably easier to read the posts. ;)
So let’s get started!
React from first principles
An element in React describes what should be rendered in the UI.
const x = <span>Hello World!</span>These elements are immutable since you cannot modify them after they are created. So what can you do with immutable elements? Pass them to functions of course!
Let’s look at three pure functions that take in an element and outputs another element. We say that these functions are pure because they do not have any observable side-effects – just data in, and data out.
const uppercase = element => (
<span style={{ textTransform: 'uppercase' }}>{element}</span>
)
const clap = element => (
<span>👏 {element} 👏</span>
)
const emphasize = element => (
<span style={{ fontStyle: 'italic' }}>{element}</span>
)A bit of theory:
The type for an element is React.Element, which are objects in category theory.
Other examples of objects are String, Boolean, etc.
The pure functions uppercase, clap,
and emphasize are morphisms in category theory. A morphism is a mapping between two objects --
in this case React.Element -> React.Element.
We can also create computations that allows us to capture data in our elements.
const Greeting = ({ name }) => <span>Hello {name}!</span>Nothing fancy here. Just a plain old functional component in React. You could render it
via JSX <Greeting name="Alice"/>, but I prefer to treat it as a normal function for now
– Greet({ name: 'Alice' }).
Now we’re ready for our first contrived example!
import ReactDOM from 'react-dom'
function contrivedEx(name) {
const a = Greeting({ name })
const b = uppercase(a)
const c = emphasize(b)
const d = clap(c)
return d
}
ReactDOM.render(contrivedEx('alice'), document.querySelector('#root'))This will render “👏 HELLO ALICE! 👏” on the screen.
The function contrivedEx has two responsibilities:
- Run the computation
Greetingto get an element out. - Map the resulting element through multiple functions, then returning the final result.
Let’s formalize these two concepts.
Look at my shiny new box!
We can wrap the original Greeting computation in a box, which I will call View.
const View = computation => ({
fold: props => computation(props)
})
// Throw in some computation, and now we have a boxed value`.
const greeting = View(({ name }) => <span>Hello {name}!</span>)To get the value out of the box, we just need to fold it.
greeting.fold({ name: 'Alice' }) // <span>Hello Alice!</span>As you can see, the fold function let’s us extract the value out of the box.
Hmm, but now when we want to map over our elements, we have to keep folding it down.

This is very tedious, so let’s define a mapping function that can operate on the values within our boxes.
const View = computation => ({
// I've shortened this since `props => computation(props)` is the same as `computation`
fold: computation,
map: f => View(props => f(computation(props)))
})The map function will return a brand-new box that runs the original computation
through the provided function f. Note that map is pure a function, and we
can still maintain a reference to the original box.
const superGreeting = greeting
.map(uppercase)
.map(emphasize)
.map(clap)
superGreeting.fold({ name: 'Alice' }) // <span>👏 <span style={{ fontStyle: 'italic' }}><span style={{ textTransform: 'uppercase' }}><span>Hello Alice!</span></span></span> 👏</span>
// Our original box is unmodified.
greeting.fold({ name: 'Alice' }) // <span>Hello Alice!</span>All computations are delayed until we call the fold function. This is a really useful property since we
can perform multiple transformations without needing to work with concrete values.
We can visualize map as follows.
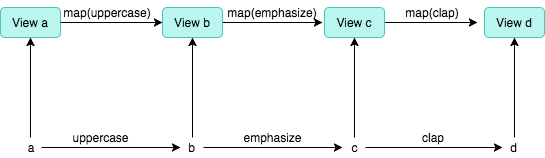
The morphisms can operate on values (elements), or we can bring them into the world of boxes (Views) and map from box to box. You can extract an element at any point by folding it down, but now we don’t have to until we really need it!
A bit of theory:
The View box that we just create is called a Functor in category theory. You can think of
functors as any object that provides the map function.
There are two mathematical laws that functors must obey:
- Identity:
a.map(x => x) === a - Composition:
a.map(x => f(g(x)) === a.map(g).map(f)
We can use these laws to our advantage when composing applications. For example,
our previous superGreeting view can be optimized by calling map
only once, using the composition compose(clap, emphasize, uppercase).
Because of the composition law, we know that Greeting.map(uppercase).map(emphasize).map(clap)
is identical to Greeting.map(compose(clap, emphasize, uppercase)).
While we’re at it, let’s also make the View a Pointed Functor by allowing us to make a single value into
a View using the View.of function.
View.of = x => View(() => x)
// Folding the view back down from a `View.of` just returns the original element.
View.of(<span>Hello</span>).fold() // <span>Hello</span>A quick aside on compose. I’m using a library called Ramda that provides a lot of
utilities for functional programming, include compose. The composition is applied from right-to-left,
so f(g(x)) is the same as compose(f, g)(x). The mathematical symbol “∘” also denotes a composition –
.e.g. f ∘ g === compose(f, g).
Okay, moving on!
Formalizing higher-order component concepts
So, isn’t the View box kind of like higher-order components (HOC)? Which we already have in “normal” React.
// Normal React HOC
const red = Component => () => <span style={{ color: 'red' }}><Component/></span>
// A map in our view
const red2 = view => view.map(x => <span style={{ color: 'red' }}>{x}</span>)Here, we have two functions that when given a component or view, returns something that is like the original input, but in red.
The difference between the HOC and the View is that the latter formalizes the concept of
mapping its value through the map function.
But wait, there is something that HOCs can do that Views cannot (yet).
For example,
const withColor = color => Component => props => (
<Component {...props} color={color}/>
)The withColor HOC takes a color (e.g. red, #fff, rgb(0,0,0), etc.), then a component
that uses the color prop, and then returns a component that is the original, but with the
color prop already provided.
const Color = ({ color }) => (
<span style={{ color }}>{color}</span>
)
const Red = withColor('red')(Color)
<Red/> // <span style={{ color: 'red' }}>red</span>Whereas the red HOC is mapping over the resulting value, the withColor HOC is mapping
over the input props. And since view.map maps over the value (element), there is no chance for us
to map over the original input to a view’s computation.
So is there anything we can do?
Of course! We just need to formalize this new concept.
Mapping over inputs
Remember that the View wraps a computation defined as Props -> Element. Let’s take a look
at a concrete example with our previous color computation.
const color = View(({ color }) => (
<span style={{ color }}>{color}</span>
))
color.fold({ color: 'blue' }) // <span style={{ color: 'blue' }}>blue</span>Here, we have Props that is some data that contains color, and Element is the
resulting <span> based on the color passed in.
What we want to do now, is to map over the input props before passing them into the computation.
This can be done by defining a nifty new function called contramap.
const View = computation => ({
fold: computation,
map: f =>
View(props => f(computation(props)))
contramap: g =>
View(props => computation(g(props)))
})Note that with map we call f with the resulting value, but with contramap
we call g with the input props, and then that result is passed to the computation as input.
So, with our new function, we can do the following.
const blue = color.contramap((props) => ({ ...props, color: 'blue' }))
blue.fold() // <span style={{ color: 'blue' }}>blue</span>Awesome! We can now map over results and contramap over inputs!
A bit of theory:
The View is now also a Contravariant, in addition to being a functor. You can think of
contravariants as any object that provides the contramap function.
And just like functors, contravariants also have similar mathematical laws:
- Identity:
a.contramap(x => x) === a - Composition:
a.contramap(x => f(g(x)) === a.contramap(f).contramap(g)
The main difference between map and contramap is that composition
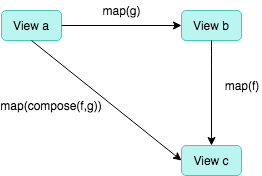
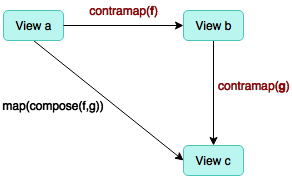
with the latter is reversed. We can visualize the difference with these two pictures
Functor composition
Contravariant composition
No need for HOCs
Now that we’ve captured both map and contramap use cases of HOCs, we no longer need them! We only need to consider
whether we are mapping over result or input to decide whether we want map or contramap.
By formalizing these concepts we can be more explicit and precise about what we are mapping over, and how we are mapping. Additionally, we have mathematical laws to help us compose our program, which is awesome!
Quick Recap
So far we’ve seen how we can:
- Put a computation of the form
Props -> Elementinto a box (View). - Take the value out via
fold. - Map over the resulting element via
map. - Map over the input props via
contramap.
But what if we want to combine multiple Views together?
Combining multiple boxes
Let’s step back from the world of React for a bit and consider an array.
const a = [1]
const b = [2]
const c = [3]We can see that arrays are functors since they implement a map function that
obeys the functor laws – you can verify this for yourself!
But arrays have something our View does not: a way to combine two arrays into a new array.
a.concat(b).concat(c) // [1, 2, 3]So let’s add this concat function to our View.
const View = computation => ({
fold: computation,
map: f =>
View(props => f(computation(props)))
contramap: g =>
View(props => computation(g(props))),
// Borrowed from Brian Lonsdord's talk Oh Composable World
// See: https://youtu.be/SfWR3dKnFIo?t=21m51s
concat: other =>
View(props => (
<React.Fragment>
{computation(props)}
{other.fold(props)}
</React.Fragment>
))
})A bit of theory:
The View is now also a Semigroup, which are objects that provide the concat function.
Semigroups have one law:
- Associativity:
(a.concat(b)).concat(c) === a.concat(b.concat(c))
Note, that View doesn't technically obey the associativity law since the ordering of the nested divs are different.
We will correct this later on in this post, but for now let's say that concat ordering is not affecting how the combined View appears on the screen.
And now we can concat like a boss!
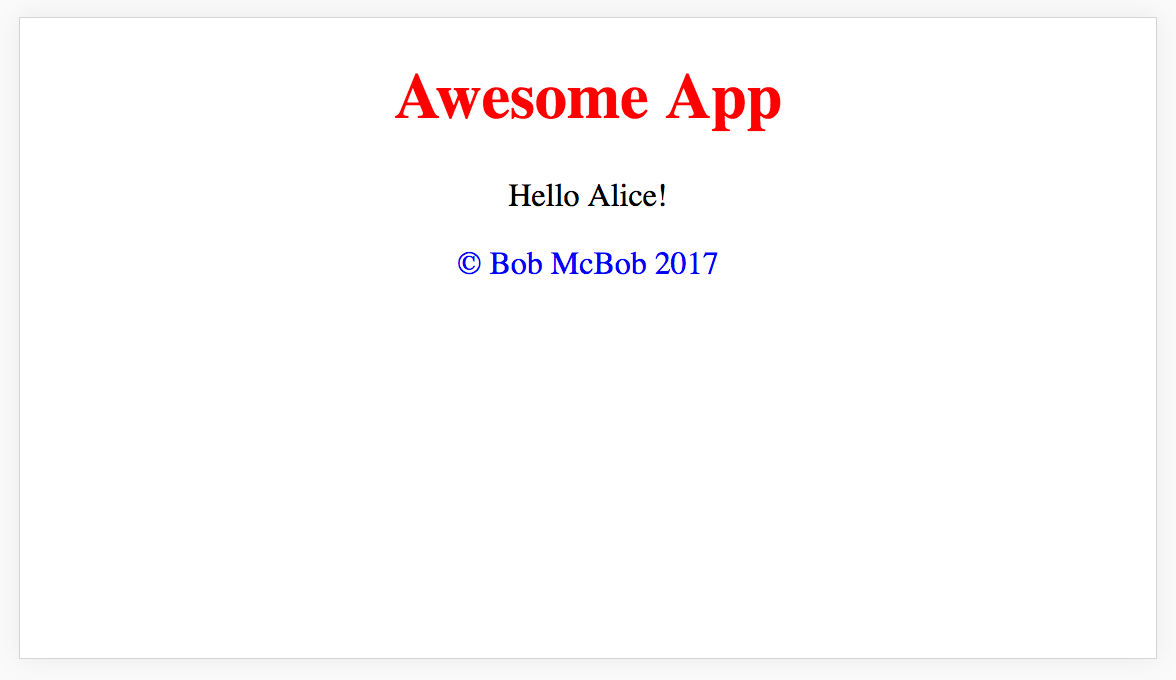
const header = View.of(<h1>Awesome App</h1>)
const greeting = View(({ name }) => <p>Hello {name}!</p>)
const footer = View.of(<p>© Bob McBob 2017</p>)
const main = header.map(x => <header style={{ color: 'red' }}>{x}</header>)
.concat(greeting.contramap(() => ({ name: 'Alice' })))
.concat(footer.map(x => <footer style={{ color: 'blue' }}>{x}</footer>))
const centered = main.map(x => <div style={{ textAlign: 'center' }}>{x}</div>)
ReactDOM.render(
centered.fold(),
document.querySelector('#root')
)Yes, the map and contramap are a bit gratuitous… But, if you run the program, you should see this.
Just for fun, we can also make View a Monoid by providing an empty function.
View.empty = View.of(null)A bit of theory:
The View is now a Monoid, and it provides the View.empty function that has the
following laws.
- Right identity:
a.concat(A.empty()) === a - Left identity:
A.empty().concat(a) === a
Remember how we filtered out null values that result from the computation? This is why the right
and left identity laws hold. Otherwise, React will generate HTML comments for null children, thus resulting
in different markup.
Summary
Phew! I think this is a good stopping point for this post. Let’s see what we’ve done so far.
- We added a new “box” called View that holds a computation to generate a React element.
- We added a
foldfunction that extracts a value out of the box. - We added a
mapfunction that maps over the value in the box. - We added a
contramapfunction that maps over the input in the box. - We added a
concatfunction that combines two boxes together.
And along the way we learned about Functors, Contravariants, Semigroups, and Monoids.
But we are not done yet since our View still hasn’t recreated two key features of React components: context and state.
In the next post, we will replicate the React context using the Reader monad.
For more resources on related functional programming topics, I recommend the following:
- Functional Programming Jargon
- Functors, Applicatives, And Monads In Pictures by Aditya Bhargava
- Oh Composable World! (video) by Brian Lonsdorf
- Professor Frisby Introduces Composable Functional JavaScript (course) by Brian Lonsdorf
- Brian Lonsdorf on Medium and Twitter